Jérémie Szeftel

Jérémie Szeftel est le lauréat 2009 du Prix de la Fondation. Il est actuellement chargé de recherche CNRS au Département de Mathématiques et Applications de l’Ecole Normale Supérieure.
"Je suis actuellement chargé de recherche CNRS au département de mathématiques et applications de l’Ecole Normale Supérieure. Mes recherches portent sur les équations aux dérivées partielles non linéaires et plus particulièrement sur les équations de la relativité générale et l’équation de Schrödinger non linéaire.J’ai reçu le prix jeune chercheur de la Fondation Sciences Mathématiques de Paris en 2009. J’étais à l’époque Instructor au département de mathématiques de l’université de Princeton.
Ce prix m’a permis de rentrer en France avec ma famille dans des conditions idéales. En effet, le retour de l’étranger pour un chercheur français n’est pas toujours facile. Grâce à la FSMP, j’ai pu disposer immédiatement d’un appartement de fonction situé très près de mon laboratoire d’accueil, et j’ai été grandement aidé par son personnel dans les inévitables démarches administratives (déménagement à partir des USA, crèche pour mon enfant, inscription à la sécurité sociale…).
J’ai également pu bénéficier d’un crédit de fonctionnement de 5000 euros disponible immédiatement, ce qui est très utile lorsqu’on ne bénéficie plus de financement dans le pays de départ, et qu’on n’a pas encore eu le temps d’en demander dans le pays d’arrivée. Ceci m’a permis en particulier d’acheter un ordinateur portable et des livres, et de couvrir mes frais de déplacements lors de conférences et de collaborations.
Enfin, j’ai eu l’opportunité de donner un cours de 20 heures sur mes recherches au Collège de France entre mars et mai 2010.
En conclusion, la FSMP a joué un rôle important dans mon retour en France, et a fait en sorte que celui-ci se passe très bien. "
Jérémie Szeftel (lauréat 2010 du Prix de la FSMP), mars 2011
Louis Dupaigne
Louis Dupaigne a bénéficié d'une invitation financée par la Fondation Sciences Mathématiques de Paris pour assister au trimestre Singularities in mechanics, au Centre Emile Borel.
 « Je crois être un bon exemple du maître de conférences lambda : j'appartiens à un labo de province ni très grand ni tout petit, je suis encore dans la case "jeunes" mais plus pour longtemps, je manque toujours de temps pour me consacrer autant que je le souhaiterais à mon travail de chercheur.
« Je crois être un bon exemple du maître de conférences lambda : j'appartiens à un labo de province ni très grand ni tout petit, je suis encore dans la case "jeunes" mais plus pour longtemps, je manque toujours de temps pour me consacrer autant que je le souhaiterais à mon travail de chercheur.
Ce trimestre à l'IHP est donc une aubaine pour moi. D'abord, l'offre de cours et séminaires est pléthorique et variée : il s'agit ici de l'étude des singularités en mécanique. J'y retrouve la petite branche des EDP (équations aux dérivées partielles) qui m'est familière, mais aussi des choses que je connais moins, voire pas du tout, notamment lorsque ce sont des mécaniciens ou des physiciens qui parlent. Ensuite, je bénéficie de deux choses qui me sont très précieuses et rares : l'accès à une bibliothèque de tout premier rang et un bureau calme, où je peux me consacrer à la recherche.
Concrètement, ce trimestre me permet de me cultiver (la propagation des singularités étant le thème le plus riche pour moi) et d'avancer à grand pas dans un projet qui m'est cher : la rédaction d'un livre (sur les singularités dans les EDP elliptiques). »
Louis Dupaigne, avril 2008
http://www.lamfa.u-picardie.fr/dupaigne/
Joel Lebowitz
Joel Lebowitz a été pendant trois semaines l’invité de la Fondation Sciences Mathématiques de Paris pour assister au trimestre Mécanique Statistique, Probabilités et Systèmes de Particules qui se déroulait au Centre Emile Borel du 5 Septembre 2008 au 19 Décembre 2008.
Aujourd’hui Professeur titulaire de la chaire George William Hill au département de mathématiques de la Rutgers University (New Jersey), Joel Lebowitz est un chercheur de grand renom qui a obtenu, au fil de sa riche carrière, de nombreux prix et distinctions : la Médaille Boltzmann (1992), le prix Henri Poincaré (2000), la Médaille Nicholson de la Société Américaine de Physique (1994), le Prix Volterra (2001), la Médaille Max-Planck (2007)…
Joel Lebowitz est, en particulier, un spécialiste de tout premier plan en mécanique statistique, un domaine à la croisée de la physique et des mathématiques, en lien avec les séries de probabilités, les systèmes dynamiques ainsi que d’autres branches des mathématiques. Il fut d’ailleurs le fondateur, en 1975, d’une des revues les plus renommées dans cette discipline : le Journal of Statistical Physics.
La mécanique statistique s’intéresse à la relation qui existe entre l’état d’un système macroscopique et les propriétés des éléments microscopiques qui le constituent (par exemple, comment la température de l’eau en ébullition dépend de la pression).
Un certain nombre de technologies modernes sont basées sur la compréhension de telles propriétés : par exemple pourquoi certains matériaux deviennent superconducteurs à basses températures, alors que d’autres non.
En d'autres termes, il s’agit d’étudier le comportement collectif d’un grand nombre d’éléments individuels relativement indépendants, mais qui interagissent entre eux. Ainsi, l’ébullition (ou le gel) sont des manifestations d’un phénomène collectif : les atomes en soi ne changent pas, les molécules, individuellement, non plus, mais leurs interactions, oui.
On constate que de nombreux aspects d’un phénomène collectif ne dépendent pas des détails. Par exemple, bien qu’une molécule d’huile et une molécule d’eau soient tout à fait différentes, un flot d’huile et un flot d’eau se comportent sensiblement de la même façon. Certaines propriétés sont donc universelles car elles ne dépendent que de lois générales de conservation. « Nous essayons ici de comprendre ces phénomènes à travers des exemples très simples », explique Joel Lebowitz. « Et souvent les résultats obtenus pour ces modèles simples sont applicables aux systèmes réels. »
Observons par exemple une transition de phase liquide-vapeur. Lors d’une telle transition, il existe une température critique Tc à laquelle on ne peut pas distinguer le liquide de la vapeur. Quand on est proche de cette température critique Tc, la différence entre la densité de liquide ?l et la densité de vapeur ?v est très faible et ne dépend ne dépend que la différence entre la température T et la température critique Tc. On écrit que :
?? = ?l – ?v ? (Tc – T)?
Or, si cette température Tc dépend du liquide, le nombre ? est, quant à lui, universel : il ne dépend pas du liquide, mais de la symétrie et de la dimension. Voilà donc un exemple de propriété universelle évoquée ci-dessus.
La mécanique statistique trouve des applications dans des domaines variés : les transitions de phase liquide-vapeur ou solide-liquide, comme on vient de le voir, mais aussi certains phénomènes sociaux, certains phénomènes biologiques, les marchés financiers, le trafic routier (comment passe-t-on d’une circulation fluide à un embouteillage), … Les individus observés peuvent donc aussi bien être des bactéries, des atomes ou des voitures, mais leur comportement collectif est déterminé par leurs interactions et peut être universel.
Rachid Belfadli
 Les vidéos des conférences et des cours proposés par la Fondation sont regardées par de nombreux chercheurs et étudiants, en France et à l'étranger. Rachid Belfadli, enseignant-chercheur au Maroc, est l'un d'eux.
Les vidéos des conférences et des cours proposés par la Fondation sont regardées par de nombreux chercheurs et étudiants, en France et à l'étranger. Rachid Belfadli, enseignant-chercheur au Maroc, est l'un d'eux.
"Je m'appelle Rachid Belfadli, je suis enseignant-chercheur à la Faculté Polydisciplinaire de Taroudant de l'université Ibn Zohr d'Agadir au Maroc. Je suis heureux d'avoir pu suivre le cours Approximation gaussienne à l’aide du calcul de Malliavin d'Ivan Nourdin à travers les vidéos que vous avez mises en ligne.
J'ai beaucoup apprécié ce cours, très bien présenté, parce qu'il m'a permis de mieux comprendre les traveaux déja publiés dans cette direction et aussi de suivre de près les dévelopments de la théorie du calcul stochastique des variations et ses applications.
J'en profite pour féliciter le Professeur Ivan Nourdin pour sa brillante réussite."
Rachid Belfadli, mars 2012
Gérard Besson
Gérard Besson (CNRS UMR 5582), organisateur du trimestre Ricci curvature and Ricci flow, explique :
“Le trimestre à part entière se déroule du 14 avril au 30 juin. L’objectif est d’amener de jeunes doctorants ou post-doctorants à suivre les colloques qui auront lieu en juin. Ainsi, du 14 avril au 30 mai, ils ont la possibilité de suivre un mois et demi de cours intensifs de préparation. Chaque session de cours se déroule sur 15 jours. En avril, ce sont des cours de base, du style de ce que l’on pourrait faire au niveau M2 Recherche. En mai, on aborde les choses à un niveau plus avancé, voire même, pour certains sujets, à la limite de ce qui est actuellement connu.
Plus d’une centaine d’étudiants sont inscrits à ce trimestre. La publicité a été faite auprès d’écoles doctorales (Chevaleret, ENS Lyon, Orsay...), avec notamment la possibilité que des étudiants valident ces cours dans leur cursus. Quelques étudiants étrangers (ayant en général bénéficié de bourses) sont également inscrits.
Il n’existe pas d’autres programmes de ce type en France. A Grenoble, il y a certes une école d’été de 3 semaines, mais l’organisation d’un trimestre nécessite des ressources en termes d’argent, d’infrastructures, de personnes, ..., qui font des programmes du Centre Emile-Borel des événements assez uniques en leur genre.”
Gérard Besson
Angelina Roche
 Après être entrée sur concours 3ème année à l’antenne de Bretagne de l’ENS de Cachan en 2009, j’ai obtenu l’agrégation de mathématiques en 2010. Je me suis ensuite orientée vers un master recherche à l’ENS de Lyon et commencé une thèse en 2011 à l'Université Montpellier II, sous la direction d’Elodie Brunel et André Mas. J’ai ensuite travaillé en tant qu’Attachée Temporaire d’Enseignement et de Recherche à l’Université Paris Descartes, avant d’être recrutée comme Maître de Conférence au CEREMADE.
Après être entrée sur concours 3ème année à l’antenne de Bretagne de l’ENS de Cachan en 2009, j’ai obtenu l’agrégation de mathématiques en 2010. Je me suis ensuite orientée vers un master recherche à l’ENS de Lyon et commencé une thèse en 2011 à l'Université Montpellier II, sous la direction d’Elodie Brunel et André Mas. J’ai ensuite travaillé en tant qu’Attachée Temporaire d’Enseignement et de Recherche à l’Université Paris Descartes, avant d’être recrutée comme Maître de Conférence au CEREMADE.
Le sujet de ma thèse portait sur la statistique pour données fonctionnelles, qui est une branche de la statistique dont l’objectif est de traiter des données sous forme de courbe (courbe de température, de consommation d’électricité, de concentration en ozone,…). Avec mes directeurs de thèse, puis en collaboration avec Gaëlle Chagny (Université de Rouen), nous avons proposé des procédures de sélection des paramètres intervenant dans les procédures d’estimation ou de prédiction (par exemple lorsque nous cherchons à déterminer la composition chimique d’un échantillon d’eau à partir de sa courbe spectrométrique). Contrairement aux procédures utilisées couramment en pratique, comme la validation croisée, nous obtenons des garanties théoriques sur l’estimateur obtenu à partir du paramètre sélectionné. De plus, nous avons constaté que, sur des données simulées, les procédures proposées sont au moins aussi performantes que les procédures usuelles mais permettent de réduire considérablement les temps de calcul des estimateurs.
Depuis ma thèse, tout en continuant à travailler sur les données fonctionnelles, je m'intéresse également à d’autres types de données (données de survie et données post-génomiques).
Olivier Lopez
 Après une thèse au CREST-ENSAI et à l'IRMAR (université Rennes 1), j'ai d'abord été recruté en 2008 comme maître de conférences au Laboratoire de Statistique Théorique et Appliquée (LSTA) de l'Université Pierre et Marie Curie. Mes thèmes de recherche, qui concernaient l'étude statistique des modèles de durée, m'ont conduit à m'orienter vers les mathématiques appliquées à l'actuariat.
Après une thèse au CREST-ENSAI et à l'IRMAR (université Rennes 1), j'ai d'abord été recruté en 2008 comme maître de conférences au Laboratoire de Statistique Théorique et Appliquée (LSTA) de l'Université Pierre et Marie Curie. Mes thèmes de recherche, qui concernaient l'étude statistique des modèles de durée, m'ont conduit à m'orienter vers les mathématiques appliquées à l'actuariat.
Devenu membre de l'Institut des Actuaires en 2011, j'ai dirigé de 2013 à 2015 la voie actuariat de l'ENSAE Paris-Tech. Je me suis notamment investi dans l'étude des phénomènes de dépendance de variables temporelles (théorie des copules) et des questions posées par les problématiques de grandes masses de données en assurance.
J'ai été recruté comme Professeur à l'Université Pierre et Marie Curie en septembre 2015, affecté au LSTA. Puis j'ai été nommé directeur de l'Institut de Statistique de l'Université de Paris (ISUP) en janvier 2016. Je travaille actuellement sur l'amélioration des techniques de provisionnement en assurance, via l'utilisation de données statistiques qui sont aujourd'hui plus faciles d'accès dans ce domaine. L'originalité des techniques développées est de réduire les frais d'expertises des compagnies, tout en améliorant considérablement la précision de la prédiction de leur charge de sinistres.
Pierre Youssef
 J’ai effectué ma thèse au sein du Laboratoire d’Analyse et de Mathématiques Appliquées (LAMA) à l’université Paris-Est Marne-La-Vallée sous la direction d’Olivier Guédon. Le titre de ma thèse était Invertibilité restreinte, distance au cube et covariance de matrices aléatoires et je l’ai soutenue le 21 Mai 2013. J’ai également reçu le prix de thèse de l’université Paris-Est pour mon travail et j’ai pu effectuer un séjour postdoctoral de deux ans à l’université d’Alberta au Canada dans le cadre du programme CNRS/PIMS avant d’être recruté en Septembre 2015 comme maître de conférences au LPMA à l’université Paris-Diderot.
J’ai effectué ma thèse au sein du Laboratoire d’Analyse et de Mathématiques Appliquées (LAMA) à l’université Paris-Est Marne-La-Vallée sous la direction d’Olivier Guédon. Le titre de ma thèse était Invertibilité restreinte, distance au cube et covariance de matrices aléatoires et je l’ai soutenue le 21 Mai 2013. J’ai également reçu le prix de thèse de l’université Paris-Est pour mon travail et j’ai pu effectuer un séjour postdoctoral de deux ans à l’université d’Alberta au Canada dans le cadre du programme CNRS/PIMS avant d’être recruté en Septembre 2015 comme maître de conférences au LPMA à l’université Paris-Diderot.
Mes intérêts scientifiques ont débuté en géométrie asymptotique, qui consiste à analyser des objets géométriques en grande dimension. Je me suis également intéressé aux problèmes de sélection de données que j’ai pu utilisé pour aborder des questions en géométrie asymptotique. C’est par cette porte que je me suis aussi tourné vers les matrices aléatoires et les inégalités de concentration.
Récemment, j’ai effectué un travail portant sur l’invertibilité de la matrice d’adjacence d’un graphe aléatoire d-régulier. Les graphes servent par exemple à modéliser les réseaux de communications et les liens entre pages internet. L’intérêt pour ces objets est donc grandissant. La matrice d’adjacence d’un graphe est un tableau de données qui indique les liens entre les sommets du graphe. Dire qu’un graphe est d-régulier signifie que chaque membre du réseau est connecté à exactement d autres membres. Etablir certaines propriétés de cette matrice d’adjacence s’avère être important pour comprendre la structure du graphe. Avec A. Litvak, A. Lytova, K. Tihkomirov et N. Tomczak-Jaegermann, nous montrons que la matrice d’adjacence d’un graphe aléatoire dirigé d-régulier est inversible avec une probabilité qui tend vers 1 quand d tend vers l’infini. Ceci répond partiellement à une conjecture posée par V. Vu et mentionnée à deux reprises lors du dernier Congrès international des Mathématiciens, à Seoul, en 2014.
Gilles Wainrib
Après une thèse à l’interface math-bio sur le rôle du bruit dans le traitement de l’information par les neurones, je me suis intéressé, lors de mon postdoc à Stanford, aux algorithmes d’intelligence artificielle qui s’inspirent du vivant, en particulier en utilisant le hasard et le désordre au coeur de leur processus de fonctionnement. Depuis mon retour en France, d’abord à l’Université Paris 13 au LAGA, puis à l’ENS au département d’informatique, j’ai également développé plusieurs collaborations avec des biologistes et des médecins pour l’étude des réseaux d’interactions biologiques en vue d’une meilleure compréhension du fonctionnement du vivant et d’applications à la médecine personnalisée.
Un problème récent : la prédiction de la réponse à un médicament
Le problème est le suivant : la colite aigüe grave est une maladie sévère qui nécessite une évaluation rapide du traitement le plus adapté. Deux traitements sont possibles et il n’existe pour l’instant aucun moyen pour les médecins de savoir quel médicament donner en première ligne.
Pour résoudre ce problème, nous avons conçu un algorithme prédictif qui combine des données cliniques (obtenues via un questionnaire) avec des données épigénétiques (micro ARN) afin de prédire de manière personnalisée la réponse au traitement. Ce travail a été effectué en collaboration avec Ian Morilla, Mathieu Uzzan, Xavier Treton, Eric Ogier-Denis. Un brevet INSERM Transfert est en cours de finalisation.
Emeric Bouin
 J’ai été recruté en septembre 2015 comme maître de conférences au CEREMADE, le laboratoire de mathématiques de l’université Paris-Dauphine. Je travaille au sein de l’équipe d’analyse. J’ai auparavant soutenu ma thèse à l’Ecole Normale Supérieure de Lyon en décembre 2014. Mon directeur de thèse était Vincent Calvez. Mes intérêts scientifiques sont l’analyse théorique et numérique d’équations aux dérivées partielles ayant des liens avec la physique et la biologie. Je cherche notamment à obtenir des résultats qualitatifs et quantitatifs sur des modèles provenant d’applications concrètes. Par exemple, une partie de mon travail de thèse est inspirée par la spectaculaire invasion de crapauds buffles en Australie. Pour moi, les mathématiques sont un bon moyen d’échange, de partage et de communication.
J’ai été recruté en septembre 2015 comme maître de conférences au CEREMADE, le laboratoire de mathématiques de l’université Paris-Dauphine. Je travaille au sein de l’équipe d’analyse. J’ai auparavant soutenu ma thèse à l’Ecole Normale Supérieure de Lyon en décembre 2014. Mon directeur de thèse était Vincent Calvez. Mes intérêts scientifiques sont l’analyse théorique et numérique d’équations aux dérivées partielles ayant des liens avec la physique et la biologie. Je cherche notamment à obtenir des résultats qualitatifs et quantitatifs sur des modèles provenant d’applications concrètes. Par exemple, une partie de mon travail de thèse est inspirée par la spectaculaire invasion de crapauds buffles en Australie. Pour moi, les mathématiques sont un bon moyen d’échange, de partage et de communication.
Mireille Bousquet-Mélou, une chercheuse à la croisée des chemins
Mireille Bousquet-Mélou est directrice de recherche CNRS au Laboratoire Bordelais de Recherche en Informatique (LaBRI), le laboratoire d’informatique de l’Université de Bordeaux. Cette année, elle a été récompensée de la Médaille d’argent du CNRS. Portrait d’une chercheuse dont les travaux se situent entre les mathématiques et l’informatique…
Spécialiste de combinatoire énumérative
Le domaine de recherche de Mireille Bousquet-Mélou se nomme la combinatoire énumérative. Concrètement, cela consiste à compter, à dénombrer, à trouver les formules qui décrivent le nombre de ceci ou de cela. Par exemple, une formule bien connue est celle des coefficients binomiaux Cnk, qui donne le nombre de manières de choisir k éléments parmi n.
![]()
La combinatoire énumérative possède des interactions à la fois avec l’informatique, en particulier l’analyse de l’efficacité des algorithmes, et avec différents domaines des mathématiques, comme par exemple l’algèbre, notamment la représentation des groupes classiques, ou encore les probabilités discrètes. « C’est ce qui me plaît dans ce domaine de recherche : la variété des outils utilisés, des domaines d’interaction », s’enthousiasme Mireille Bousquet-Mélou. « C’est un domaine qui fait feu de tout bois ! »
Des chemins sur une grille carrée
Prenons une grille carrée sur laquelle on peut « marcher » dans n’importe quelle direction (haut, bas, droite ou gauche) en suivant les lignes. Un exemple de problème de combinatoire énumérative consiste à se demander combien de chemins ne se recoupant pas et ayant un nombre de pas fixé n on peut y tracer.
Pour n = 1 il y a 4 chemins possibles.
Pour n = 2, il y en a 12.
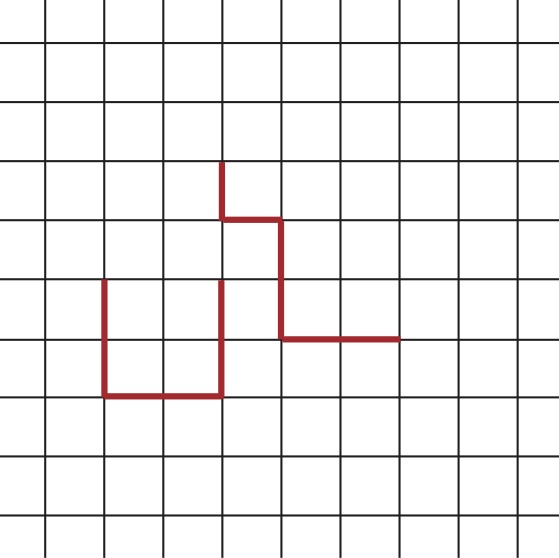
Deux chemins pour n = 6
« On ne connaît pas de formule générale donnant le nombre de chemins pour tout n », nous apprend Mireille Bousquet-Mélou avant de préciser que « si une telle formule existe, elle n’est probablement pas simple ».
Une autre question irrésolue depuis des décennies, qui intéresse les probabilistes, est la suivante : si on prend un chemin de longueur n au hasard, quand n est grand, à quelle distance le point d’arrivée se trouve-t-il du point de départ ?
« Ces problèmes possèdent aussi des liens avec la physique statistique », ajoute-t-elle. « Les chemins en question peuvent être pensés comme des polymères. »
Pour sa part, elle travaille notamment sur des questions similaires : « Des chemins auto-évitants, mais aussi des problèmes de chemins en 2D ou 3D, qui peuvent se couper mais sont contraints à rester dans une portion de l’espace. Ce sont des problèmes de dénombrement mais qui comportent aussi un peu de calcul formel. »
La vocation tranquille
De son enfance à Pau, Mireille Bousquet-Mélou se souvient avoir été « le modèle de la bonne élève », mais pas d’une vocation précoce pour les mathématiques : « J’avais de bonnes notes partout et aucune idée de ce que je voulais faire plus tard. » Elle s’oriente en classe préparatoire scientifique – qu’elle effectue à Toulouse – et intègre l’ENS, à Paris, à l’automne 1986. Elle y fait un DEA entre probabilités et statistiques, et découvre la combinatoire énumérative grâce à un cours « pétillant » de Xavier Viennot. Sous sa direction, elle commence par faire une thèse sur le dénombrement des polyominos.

Polyominos à 1, 2, 3, 4 ou 5 cases
« Quelques années après ma thèse », poursuit-elle, « j’ai eu la chance de tomber, grâce à un collègue, sur un très joli sujet qui concernait le dénombrement de certaines partitions d’entiers, avec des conditions originales sur les parts… L’occasion de trouver de belles formules. C’est un sujet qui a eu de la descendance. »
Au contact de Philippe Flajolet, qui a fédéré une communauté française de spécialistes de combinatoire, des probabilités, d’analyse d'algorithmes, elle s'intéresse aussi au dénombrement asymptotique.
Plusieurs séjours en Australie auprès de physiciens statisticiens lui donnent l’occasion de s’ouvrir à d’autres domaines, de formuler des questions autrement, d’explorer d’autres sujets : « C’est à ce moment-là que j'ai commencé à m'intéresser aux chemins auto-évitants. »
Dans sa discipline, les questions viennent souvent d’autres domaines des mathématiques : « Parfois, ces questions existent indépendamment dans plusieurs disciplines différentes. Par exemple, les chemins auto-évitants appartiennent autant à la combinatoire et aux probabilités qu’à la physique statistique. »
« Chatouiller le cerveau »
« Ce que j’aime dans la recherche en mathématiques », confie Mireille Bousquet-Mélou, « c’est que ce n’est jamais ennuyeux. Ça chatouille le cerveau. C’est prenant et stimulant. » Elle voit sa discipline comme « un jeu à très grande échelle », pour lequel il faut s’armer de persévérance, de ténacité et de patience : « On sèche la plupart du temps mais il y a aussi des moments où l’on sent que l’on est en train d’avancer, sans savoir où et comment. On entrevoit que l’on est sur le point de comprendre quelque chose. On est le siège d’une petite alchimie. C’est très intrigant. » Pour la chercheuse, la manière dont viennent les idées reste souvent un mystère : « Parfois, on découvre que la bonne façon de faire était en fait très simple. On se demande : mais pourquoi n’ai-je pas formulé ça de cette façon avant ? » Elle se souvient : « Il m’est déjà arrivé de me lever un matin en ayant enfin compris comment résoudre un point sur lequel je butais. C’est très curieux et ce caractère étrange a beaucoup de charme. »
Elle regrette que les mathématiques souffrent d’une image si effrayante : « En France, les mathématiques sont présentées comme le truc qu’il faut absolument savoir faire. Forcément, ça attire certaines personnes, mais ça en rebute beaucoup d’autres. Je crois qu’il faudrait laisser les gens s’approprier les maths, s’amuser avec. »
Les récompenses
Avant sa Médaille d’argent du CNRS, Mireille Bousquet-Mélou avait déjà été distinguée par la Médaille de bronze, ainsi que par un prix de l’Académie des Sciences en mathématiques. Ce qui n’a pas empêché sa surprise et son émotion à la réception de cette nouvelle récompense prestigieuse. « L’initiative émanait de l’INSMI – NDRL : l’institut de mathématiques du CNRS -, un institut qui n’est pas le mien puisque je travaille dans un laboratoire d’informatique », explique-t-elle, avant d’ajouter : « Être entre deux disciplines n’est pas toujours confortable, cela comporte certains attraits mais aussi quelques inconvénients. Cette récompense est une reconnaissance pour moi mais aussi pour mon domaine, qui est ainsi mis en lumière. »
Une distinction qui, peut-être, contribuera également à encourager des jeunes femmes sur la voie des mathématiques ou de l’informatique fondamentale. « C’est un constat de fait : il y a encore peu de femmes dans les mathématiques. L’informatique théorique n’est pas trop mal lotie en France, par rapport à d’autres pays (en 2012, en informatique, elles représentaient 23% des effectifs totaux des CR et DR du CNRS d'après les chiffres de l'INS2I, 26% des maîtres de conférence et 19% des professeurs). Ceci dit, je suis la seule femme de mon groupe, au LaBRI. » Et de conclure : « Je ne vois guère de changement pour l’avenir proche. Je crois que ce sont des évolutions qui viennent très lentement. »
Propos recueillis par Gaël Octavia
Juin 2014
Autour de Wolfgang Döblin et du mouvement - Rencontre avec Marc Yor
Membre de l’Académie des Sciences, Professeur à l’Université Pierre et Marie Curie depuis 1981, Marc Yor effectue ses recherches au Laboratoire de Probabilités et Modèles Aléatoires (LPMA). Depuis le début de sa carrière – il a soutenu sa thèse de 3e cycle en 1973, puis sa thèse d’Etat en 1976 - il s’intéresse au calcul stochastique, et plus spécialement aux martingales, qui sont un type particulier de processus aléatoires « en équilibre », et au mouvement brownien.
Mouvement brownien
Après sa thèse de 3e cycle, Marc Yor a essayé de s’orienter vers la physique théorique avant de découvrir l’univers passionnant du mouvement brownien. « J’avais commencé, pendant un an, par faire de la théorie quantique des champs, notamment dans le cadre du programme de Symanzik. Ce programme demandait de connaître des propriétés fines du mouvement brownien plan. J’ai donc décidé d’étudier ce domaine et j’y suis resté. » Il observe par exemple la façon dont la trajectoire du mouvement brownien plan s’enroule autour d’un nombre fini de points. « On fait l’étude asymptotique de ces enroulements, c’est-à-dire que l’on regarde comment cela se passe lorsque le temps tend vers l’infini » explique-t-il. « C’est une question sur laquelle j’ai passé beaucoup de temps entre 1977 et 1989. Les résultats décisifs ont été obtenus avec Jim Pitman, professeur à Berkeley, et Jean-François Le Gall, qui préparait alors sa thèse d’Etat (en 1984). »
Mathématiques financières
Bien qu’il ne se considère pas comme un spécialiste des mathématiques financières, les travaux de Marc Yor trouvent de nombreuses applications dans ce domaine. Par exemple, il s’est intéressé aux options asiatiques, qui s’expriment en termes d’exponentielles du mouvement brownien. Il relate : « Un certain nombre de gens qui travaillent en mathématiques financières m’ont posé sur le mouvement brownien des questions qu’ils rencontraient dans leur activité ». Il ajoute : « Mon intérêt, c’est le mouvement brownien lui-même, mais je suis heureux que d’autres domaines comme la finance soient à l’origine de questions intéressantes du point de vue des mathématiques. Cela apporte un angle nouveau, une approche nouvelle. »
La finance n’est pas le seul domaine à nourrir les recherches de Marc Yor : « J’ai parlé précédemment de processus continus, mais on peut aussi considérer des processus qui comportent des sauts : les processus de Lévy. Ils interviennent par exemple dans les télécommunications ou dans des questions physiques, comme la formation des galaxies. Par conséquent, je travaille aussi en contact avec des physiciens théoriciens. »
Un exemple de problème ouvert
« Considérons une certaine information accumulée jusqu’à un temps t. Il peut s’agir, par exemple, de l’information emmagasinée sur une population au cours du temps. Bien sûr, cette information augmente avec le temps. Une question est de se demander si cette famille d’informations, fonction du temps t, peut être décrite par un mouvement brownien. Si oui, on dit que c’est une information brownienne. Autrement dit, un processus peut coder une famille d’informations. Il s’agit alors de classifier ces familles d’informations : je me demande en particulier si telle famille est brownienne ou pas. A l’heure actuelle on a des conditions nécessaires pour dire si c’est le cas mais pas de conditions nécessaires et suffisantes. Boris Tsirelson, actuellement en Israël après avoir vécu et travaillé en Union Soviétique, a permis de réaliser beaucoup de progrès sur ces questions. »
Allers-retours entre deux domaines mathématiques
D’autres domaines des mathématiques peuvent être une source de questions pour les probabilistes. La théorie des nombres en est un exemple. Ainsi, les nombres premiers étant distribués de manière erratique, on peut se demander s’il existe un (ou des) modèle(s) probabiliste(s) qui rende(nt) compte de leur distribution. Il en existe effectivement, par exemple le modèle dit de Cramer.
Un autre problème fascinant (ayant d’ailleurs des liens étroits avec le précédent) extérieur aux probabilités mais trouvant des éclairages grâce à elles est l’hypothèse de Riemann, un problème d’arithmétique extrêmement difficile qui figure dans la fameuse liste des « sept problèmes du millénaire » distingués par la Fondation Clay. Avec les travaux par exemple de Dyson et plus récemment de Keating et Snaith, on essaie d’obtenir des avancées sur ce problème via l’étude des matrices aléatoires de grandes tailles, en faisant un aller-retour entre les deux domaines. « C’est comme s’il existait un dictionnaire entre d’un côté la fonction zêta de Riemann et de l’autre les matrices aléatoires » explique Marc Yor. Grosso modo, les questions sur la fonction zêta sont en quelque sorte « traduites », grâce à ce « dictionnaire », dans le domaine des matrices aléatoires, celles-ci étant moins difficiles à étudier. Ensuite les résultats sont « traduits » en sens inverse, c’est-à-dire du domaine des probabilités vers le domaine de la fonction zêta. « On ne sait d’ailleurs même pas pourquoi cela fonctionne si bien » admet le mathématicien. « C’est comme si deux peuples habitant deux endroits opposés sur la planète et n’ayant jamais eu de contacts l’un avec l’autre avaient élaboré des langages structurés exactement de la même manière. » Et il conclut : « C’est une des caractéristiques merveilleuses des mathématiques : deux domaines ne sont a priori pas liés entre eux et pourtant les travaux effectués dans l’un permettent d’avancer dans l’autre ! »
Le fascinant Wolfgang Döblin (1915-1940)
Marc Yor a eu la chance de participer à la publication d’un des travaux d’un mathématicien hors du commun mort en 1940 : Wolfgang Döblin.
Né en 1915, Wolfgang est le fils du médecin et grand écrivain allemand Alfred Döblin, antinazi de la première heure, auteur du célèbre Berlin Alexanderplatz porté à l’écran par Fassbinder.
Le jeune Wolfgang semble avoir très tôt témoigné de convictions politiques fortes. Ainsi, au lycée, il refuse de suivre les cours d’instruction religieuse. Plus tard, il explique avoir voulu étudier la statistique et l’économie dans un but marxiste. La famille Döblin, juive, quitte Berlin dès la Nuit de Cristal pour émigrer en Suisse, puis en France. Ils obtiendront la nationalité française. Resté dans la capitale allemande jusqu’à l’obtention de son baccalauréat, Wolfgang les rejoint à Maisons-Laffitte. Il soutient sa thèse (qui porte, grosso modo, sur l’équation de Kolmogorov et autres questions connexes) en 1938, sous la direction de Maurice Fréchet.
A 24 ans, Wolfgang Döblin est enrôlé dans la « Drôle de guerre ». Il se bat notamment en Lorraine et obtient la Croix de Guerre. Il se suicide après la capitulation de la France, le 21 juin 1940, dans une grange de Housseras, petit village des Vosges. Auparavant, il avait eu le soin, dès février 1940, d’envoyer ses travaux à l’Académie sous pli cacheté.
En 2000, ce fameux pli de Döblin est enfin ouvert après 60 années d’attente, grâce aux demandes répétées du mathématicien Bernard Bru. Marc Yor en découvre alors le contenu. « Je connaissais à peine l’existence de ce pli », se souvient-il. Il se passionne immédiatement pour le personnage de Döblin. A partir de mai 2000, il travaille donc avec Bernard Bru à la publication du pli, qui paraîtra accompagné de notes historiques et mathématiques dans un volume spécial des Comptes-rendus de l’Académie en décembre 2000.
« Döblin décrit les processus de diffusion unidimensionnels, qui modélisent une particule aléatoire qui évolue continûment au cours du temps », explique Marc Yor. « Pour cela, il utilise la notion de martingale et développe des relations entre les martingales continues et le mouvement brownien. Ces travaux complètent brillamment ceux de sa thèse ; on peut penser qu’il avait discuté de la notion de martingale à l’IHP, avec Jeanville. » Coïncidences des destinées mathématiques : on peut faire un parallèle entre Döblin et le mathématicien japonais Kiyoshi Ito, né lui aussi en 1915, mobilisé pendant la Seconde Guerre Mondiale, et qui s’est également illustré pour ses travaux de premier plan sur les processus stochastiques, dont le mouvement brownien, bien que les deux mathématiciens n’aient jamais été en contact. On notera cependant qu’Ito est mort en 2008, à l’âge honorable de 93 ans.
Dans la veine d’Abel et Galois
« Quand on a étudié le Pli Cacheté de Döblin en 2000, on s’est rendu compte que, dans le domaine couvert par le pli, ce jeune mathématicien avait 25 ans d’avance » poursuit Marc Yor. « En effet, dans le contenu de ce fameux pli, qui date donc de 1940, il développe des méthodes et des résultats (re)découverts vers 1965. » Jeunesse, œuvre mathématique exceptionnelle (écrite pour partie dans les terribles conditions de la Seconde Guerre mondiale), mort tragique, reconnaissance posthume : à bien des égards, Wolfgang Döblin rappelle Niels Abel et – peut-être encore plus, du fait de ses convictions politiques affirmées et de son tempérament – Evariste Galois. Le grand mathématicien Paul Lévy - « qui n’était pas réputé pour distribuer des compliments à tort et à travers » insiste Marc Yor – n’hésitera pas à le situer dans la catégorie de ces deux jeunes mathématiciens géniaux.
« 10 ans après l’ouverture du pli, il est émouvant de constater que l’intérêt pour les travaux et la vie de Wolfgang Döblin ne s’est pas toujours pas tari », constate Marc Yor. « Il faut cependant ajouter que ceux qui s’y intéressent le font pour des raisons très diverses. Certains sont des probabilistes, d’autres, des amateurs des romans de son père Alfred, d’autres encore manifestent une curiosité envers l’évolution spirituelle de cette famille juive convertie au catholicisme après son émigration aux Etats-Unis. » On peut notamment retrouver Döblin dans le livre de Marc Petit paru en 2003, L’Equation de Kolmogorov, ainsi que dans deux films documentaires :Wolfgang Doeblin, A Mathematician Rediscovered, d’Agnes Handwerk et Harrie Willems (DVD Springer, 2007) et La lettre scellée du soldat Döblin, de Jürgen Ellinghaus et Hubert Ferry (diffusé sur Arte en 2006).
Marc Yor a contribué à faire connaître ce mathématicien remarquable non seulement dans la communauté mathématique (la publication des œuvres complètes de Wolfgang Döblin est actuellement en cours ; ces œuvres consistent – outre le Pli Cacheté – en 13 articles et 13 Notes aux Comptes rendus, dont l’ensemble a été publié en 4 ans !) mais aussi auprès du grand public, puisqu’il lui a consacré le sujet de sa conférence du 23 janvier 2008 à la BnF, dans le cadre du cycle « Un texte, un mathématicien » destiné aux non-spécialistes. « Tout cela n’aurait pu avoir lieu sans la ténacité de Bernard Bru » rappelle Marc Yor en guise de conclusion.
Remerciements de Marc Yor
« Ils vont à Gaël Octavia qui a su transformer notre conversation très informelle en un texte qui, je l’espère, amènera encore de nouvelles personnes, mathématiciennes ou autres, à s’intéresser à divers aspects de la vie et de l’œuvre de Wolfgang Döblin.
Ils vont aussi et surtout à Bernard Bru, dont l’inlassable volonté de faire connaître les travaux de Wolfgang Döblin s’est finalement trouvé récompensée au delà de toute espérance. »
Corinna Cortes
Corinna Cortes est chercheuse en informatique et dirige Google Research, après avoir travaillé pendant plus de 10 ans dans les laboratoires AT&T Labs – Research (anciennement AT&T Bell Labs). Ses recherches portent sur les algorithmes d’apprentissage automatique, un domaine qui trouve des applications dans des outils tels que les moteurs de recherche, les systèmes de reconnaissance automatique de l’écriture ou de traitement de la parole. Elle a en particulier apporté d’importantes contributions aux bases théoriques des machines à support vectoriel ainsi qu’au data-mining (c’est à dire l’extraction de connaissances à partir de données) pour les très grandes données. Elle a notamment reçu pour ses travaux la Médaille AT&T Science and Technology en 2000 et, conjointement à Vladimir Vapnik, le Prix Paris Kanellakis Theory and Practice en 2008, deux prix importants en informatique. Propos recueillis à l'occasion de Maths A Venir 2009.
Could you describe shortly your college path and career from your first position as a researcher to present?
My path as a student was a long and windy road. Just like many other girls in high school, I took math and physics at the highest level, and really liked math. But, due to some peer pressure and other areas of interest of mine, I did a detour through theology and later Danish literature! During a break, I felt a need to identify with the working class (this was the very early eighties) and I also took a job at a factory where I met a number of engineering students. That was a great experience. I eventually changed to math and physics, and completed a Master’s degree in Denmark.
On my way to a Ph.D. program in computer science in the US, I got a summer internship at AT&T Bell Laboratories, back then one of the most prestigious research labs in the world. I didn’t really leave it the next 14 years. I was lucky enough to spend most of my student years there, only occasionally visiting my university, and after my Ph.D. degree, I stayed on as a full-time researcher.
With the rise of the Internet, new possibilities opened up, and, 6 years ago, I moved to Google Research, one of the most fascinating and energizing work places in the US.
What was your very first subject of research?
My first years at Bell Labs were spent in a machine learning group, which shaped my later carrier. A year after I got there, Vladimir Vapnik joined the group, and together we developed Support Vector Machines. That became a part of my thesis and has remained one of my main interests since then. Support Vector Machines inspired work in many other machine learning algorithms, and today I would rather say I work on “Kernel Methods”, but my work is still very related to my original thesis work.
Which problems are you currently working on?
The problem settings I am working on have changed a bit over the years.
Learning theory and algorithms were originally designed for a flawless world, somewhat perturbed by random noise. But the real world we deal with at Google is often far from that perfect ideal. In practice, data is poorly labeled or not labeled at all, data can be biased or drawn from slightly different problems than what one is trying to learn, and the distributions may drift with time. Machine learning at Google must address all these issues to be effective and obtain high-quality solutions. Disregarding these questions can lead to dramatically poor performance or lead to unpredictable results or behavior, thereby harming quality.
Another challenge facing learning applications at Google is the staggering size of the datasets, which exceeds several million and can reach billions of high-dimensional data points. Scaling exiting learning algorithms to deal with such magnitudes using massively distributed systems, or devising novel techniques taking advantage of these systems while not sacrificing learning guarantees, is an important question in many of our applications.
Could you describe to us in simple words a typical problem raised in your field of research?
Sure, let us take image search as an example. Search for images using all the major search engines is still primarily text-based. We input text, and the images returned are primarily based on the text surrounding the images. We clearly have to move towards better image understanding, building learning algorithms that can reliably recognize objects in the images. But just think of the scale of the internet, how many images are out there and how many object recognizer are needed. Think of the quality of the images. The object recognizers will have to be very robust against noise and occlusion, be able to work on low as well as high resolution images, color and black and white, etc. These are hard problems for machine learning.
Are the problems you deal with raised by practical needs or is it pure theory?
The fun thing about being at Google is that we have access to real problems and lots of data. Hence, naturally, the problems we are working on are inspired by practical needs. Otherwise, we could just as well be in academia. But we are striving to find general solutions that can work across a number of applications and produce publishable results. A good project has two major outlets: a publication and a launch. Both exciting.
Could you describe a typical application of your current work?
To solve problems in machine learning, one typically has to build a classifier from labelled data. Support Vector Machines is still one of the most popular techniques. SVMs are widely available in a number of software packages and used by most machine learning practitioners.
Do you consider yourself as a mathematician or as a computer scientist?
I am trained as a mathematician, a physicist and a computer scientist, and I think of myself as all of the above. It is really important to have good math skills to be able to prove properties about an algorithm [will it converge? Is there a unique solution? What guarantees does it give for performance on a new test point?]. It requires a lot of knowledge of optimization to effectively deal with the scale of our applications, it requires good intuition about data to know what to pursue, and it requires good computer science skills to independently develop a solution. In my group, we have primarily computer scientists, but we also have optimization people and statisticians.
Which mathematics are “hidden” (for the average user) in tools you work on?
The large-scale problems in machine learning have inspired a lot of mathematicians to work on approximation algorithms and optimization techniques. Good knowledge of algorithms is another hidden field.
What kind of unsolved problem do you find in your field of research?
How do you effectively and relatively accurately invert a million-dimensional dense matrix in seconds on an ordinary desktop computer.
Do you think that the average person needs to know or should know a few of the science behind the computing tools daily used by them?
Maybe not the average person, but I could wish the young people better realized the opportunities that lie ahead of them if they master computers and can enhance the flow of information.
Just think of a visit to the hospital, how much of our treatment is tied to recent developments in computer science. The image processing behind the MRI or x-ray we get to locate the problem, the monitoring and alerting of our vital signs, the development in computational biology and the drug industry where one can simulate and experiment with new medications using computers, the electronic records that makes our chart available to all functions of the hospital, the statistics that is aggregated to better understand the outcome of the treatment. It is sad that especially girls are not more attracted to the area.
Regards croisés de Nalini Anantharaman et Josselin Garnier
Propos recueillis à l'occasion de Maths A Venir 2009, à retrouver sur le site de Maths A Venir.
 |
 |
|
Nalini Anantharaman, 33 ans, à l’Université Paris Sud-Orsay |
Josselin Garnier, 38 ans, à l’Université Paris-Diderot |
Comment êtes-vous devenus mathématiciens ?
Nalini Anantharaman
J’ai grandi dans une famille de mathématiciens donc c’était pour moi une idée assez naturelle.Souvent, on ne pense pas que les mathématiques puissent être une carrière. Aux yeux de beaucoup de gens, être bon en maths permet de faire d’autres choses (ingénieur, par exemple), mais pas mathématicien. J’ai eu une petite hésitation entre les mathématiques et la musique (le piano), mais j’ai vite opté pour les maths.
Josselin Garnier
Chez moi, il n’y avait pas de tradition mathématique dans la famille. Ma vocation est venue plus tard. J’ai été assez tôt attiré par les domaines scientifiques – passé l’inévitable phase où je voulais être pompier – mais j’aimais plutôt la chimie. C’est à l’Ecole Normale Supérieure que j’ai découvert des mathématiques qui m’intéressaient.
Quelles sont les qualités nécessaires pour être mathématicien ?
Nalini Anantharaman
Il n’y a pas vraiment de profil. Certains mathématiciens sont des gens très organisés, d’autres très désordonnés, certains écrivent beaucoup, d’autres font des mathématiques en ayant l’air de rêvasser…
Josselin Garnier
Il suffit de voir les bureaux des mathématiciens pour comprendre qu’il en existe de tous les styles.
Nalini Anantharaman
S’il fallait trouver une qualité commune, je citerais toutefois la persévérance.
Josselin Garnier
Je suis d’accord : quand on est mathématicien, on passe 90% de son temps à explorer des fausses pistes.
Nalini Anantharaman
Il faut aussi être créatif, mais la créativité en mathématiques, ça veut dire savoir poser de bonnes questions et pas seulement savoir trouver des réponses. Il faut aussi savoir convaincre ses collègues de l’intérêt des questions que l’on pose.
Josselin Garnier
J’ajouterai aussi la capacité à ne pas avoir le nez dans le guidon, avoir du recul sur ce que l’on fait.
Comment travaille un mathématicien ?
Nalini Anantharaman
Un mathématicien essaye de démontrer des choses nouvelles. Pour cela, il doit se tenir au courant de ce que les autres ont fait. Une partie du travail consiste donc à lire des articles. A partir des travaux des autres, on trouve de nouvelles idées, on pose de nouvelles questions.
Josselin Garnier
On va à des colloques, soit pour faire des exposés, soit pour en écouter, ce qui dans les deux cas donne lieu à des discussions, à de nouvelles questions. A chaque question résolue, deux nouvelles viennent.
Nalini Anantharaman
Une partie de notre travail consiste également à encadrer des thèses. On apprend beaucoup des étudiants car eux-mêmes posent des questions et ont des idées très inattendues.
Toute la partie qui consiste à trouver des idées de questions se fait donc avec d’autres : mathématiciens, étudiants, et aussi, dans mon cas, avec des physiciens. Ensuite, vient la partie « recherche », où l’on essaye de répondre à ces nouvelles questions. Pour moi, c’est la partie solitaire, que j’effectue d’ailleurs beaucoup à la maison.
Josselin Garnier
L’idée mathématique peut venir n’importe où, à n’importe quel moment.
Nalini Anantharaman
En tout cas c’est un métier où l’on apprend sans cesse de nouvelles choses. Je suis professeur et chercheuse mais une partie de moi est une éternelle étudiante.
Collaborez-vous avec des spécialistes d’autres disciplines ?
Nalini Anantharaman
Nous travaillons tous les deux dans des domaines en lien avec d’autres disciplines, et même, pour Josselin, avec l’industrie. J’étudie l’équation de Schrödinger, qui est une des équations de base de la mécanique quantique. Je collabore avec des physiciens théoriciens.
Josselin Garnier
Quant à moi, mon travail est à l’interface entre les équations aux dérivées partielles et les probabilités. Je suis en relation avec des physiciens expérimentaux. Mes travaux touchent à des domaines où interviennent des ondes, comme l’imagerie, les télécoms…
Pouvez-vous donner un exemple de question que vous essayez de résoudre ?
Josselin Garnier
En ce moment, j’essaie d’exploiter le bruit de fond. Est-ce qu’il y a de l’information dans ces signaux qu’on appelle du « bruit » et que l’on jette ? Est-ce qu’on peut faire de l’imagerie avec ?
Nalini Anantharaman
Moi, j’essaye de comprendre les phénomènes de dispersion. Une onde se propage dans une cavité fermée. Elle va rebondir sur les parois. J’essaye de comprendre la manière dont elle va se disperser : va-elle rester cloisonnée, confinée dans une partie de la cavité ou va-t-elle se disperser dans toute la cavité ?
Qu’est-ce que vous aimez dans le métier de mathématicien ?
Josselin Garnier
J’aime beaucoup le processus de découverte, avec ses hauts et ses bas, ses surprises. J’aime ces moments où on a l’impression que l’on s’approche de la solution, où l’on ressent cette excitation très particulière, jusqu’à ce que l’on réalise que c’est une fausse piste et qu’il faut en chercher une autre. Et puis évidemment, de temps en temps, on fait une vraie découverte et c’est un moment très jouissif. On a le sentiment, pour reprendre l’expression de Descartes, d’être « maître et possesseur de la nature ».
Nalini Anantharaman
J’aime aussi le fait que, finalement, la manière dont notre cerveau fonctionne, la manière dont on raisonne, dont on aboutit à une découverte, tout cela reste mystérieux. Un autre aspect fascinant des mathématiques est que c’est un langage abstrait qui, pourtant, est reflété par la nature.
Josselin Garnier
Par exemple, vous faites une expérience virtuelle, dans votre tête ou avec un ordinateur, vous en calculez le résultat. Tout cela est abstrait. Et pourtant, lorsque vous faites cette expérience pour de vrai, dans la réalité, cela fonctionne comme vous l’aviez prévu. Cela continue à me surprendre !
Pourquoi, à votre avis, les mathématiques sont-elles si impopulaires auprès du grand public ?
Nalini Anantharaman
Les mathématiques sont victimes du rôle négatif qu’on leur fait jouer comme instrument de sélection. Les gens s’en souviennent comme d’une cause de stress ou d’échec scolaire.
Josselin Garnier
Je trouve également dommage que la vision que l’on a des mathématiques au collège, au lycée et même en classe préparatoire soit si réductrice, binaire, et n’ait rien à voir avec la réalité de la recherche. Dans un exercice scolaire, vous avez des hypothèses posées, une unique conclusion à laquelle il faut absolument arriver et l’impression qu’entre les deux, il n’y a qu’un seul chemin. La recherche c’est tout le contraire : on n’a ni hypothèse ni conclusion posées a priori, il y a mille chemins possibles et on ne connaît pas les outils qui nous mèneront à une découverte.
Nalini Anantharaman
A l’école, la solution d’un exercice tombe comme un couperet. Il manque l’idée que l’on peut faire plusieurs tentatives, il manque les notions de droit à l’erreur, de droit à recommencer…
Josselin Garnier
Dans l’enseignement, on n’explique pas aux élèves – probablement par manque de temps - que tâtonner, réessayer, changer de méthode, tout cela fait partie des mathématiques.
Nalini Anantharaman
De plus, l’erreur peut être féconde, elle peut amener à d’autres découvertes. Toute initiative est bonne !
Pensez-vous qu’il faille vulgariser les mathématiques auprès du grand public ?
Nalini Anantharaman
Oui. Les mathématiques font partie de la culture générale. Le public doit connaître un certain vocabulaire mathématique.
Josselin Garnier
Il faut que les gens voient certaines images, entendent parler de certaines théories, de certains grand problèmes de mathématiques. Mais c’est une tâche ardue ! Il faut repousser les préjugés sur le fait que les mathématiques ne peuvent pas être appréciées par le commun des mortels sauf s'il a reçu "le don" (on dirait plutôt, s'il a la bosse des maths). Il faut montrer que les mathématiques sont vivantes.
Nalini Anantharaman
Les chercheurs en mathématiques sont toujours volontaires pour tenter des animations de type « Fête de la science » ou des conférences grand public, car cela permet d'avoir une discussion directe, très stimulante avec le public. Evidemment, de nombreux chercheurs seraient volontaires pour participer à des émissions de radio ou de télé, même s'il y a une plus grande timidité vis-à-vis de ces medias. Il est toujours difficile d'expliquer un résultat mathématique.
Josselin Garnier
Je pense que cela vient du fait qu'un résultat mathématique ne peut vraiment s'apprécier qu'à travers la compréhension du chemin qu'il a fallu suivre pour l'obtenir.
Nalini Anantharaman
Dans une conférence ou une émission, on peut au mieux donner une intuition de ce que sont les objets mathématiques et de ce qu'est l'activité d'un chercheur.
Olivier Faugeras, ou l'appel des neurosciences
Ancien polytechnicien, mathématicien, spécialiste des neurosciences, membre de l’Académie des Sciences, Olivier Faugeras est Directeur de Recherche à l'INRIA (Unité de Recherche de Sophia Antipolis) et dirige NEUROMATHCOMP, un projet de recherche tourné vers la modélisation mathématique des neurones et des ensembles de neurones. Il s’intéresse plus particulièrement à la reconstruction 3D de l'activité du cerveau humain, à la vision par ordinateur, à l’analyse d’images en vue de comprendre la perception visuelle, à la neuroscience computationnelle (qui essaye de comprendre les relations entre la structure et la fonction du cerveau et du système nerveux), à l’analyse du mouvement et de la stéréoscopie… Il est professeur à l’Ecole Normale Supérieure. Il nous parle ici des liens entre mathématiques et neurosciences. (Propos recueillis à l'occasion de Maths A Venir 2009.)
Comment est venu votre intérêt pour les neurosciences ?
J’ai commencé par étudier les mathématiques. J’ai fait de la recherche en mathématiques, puis je me suis orienté vers l’informatique et plus particulièrement vers l’analyse d’images, qui est un domaine d’application des mathématiques puisqu’elle fait intervenir de la géométrie ou encore des équations aux dérivées partielles (EDP). De là, je suis arrivé aux neurosciences où les problèmes d'ordre mathématique sont immenses.
Quels sont les problèmes posés en analyse d’images ?
Ce sont par exemple des questions liées à la compression : comment coder une image de sorte qu’elle occupe le moins de place possible dans la mémoire d’un ordinateur, tout en préservant l’essentiel de son contenu.
Quel lien avec les neurosciences ?
Le plus souvent, les images compressées sont destinées à être regardées par des êtres humains donc cela pose une deuxième question : puisque l’on ne garde qu’une partie de l’information, quelle partie faut-il sélectionner pour que l’image compressée soit adaptée à la vision de l’être humain qui la regarde ? On va se calquer sur la perception visuelle humaine. On sait que quand on regarde un objet, notre cerveau effectue lui-même un filtrage de l’information : il n’en garde qu’un certain pourcentage, environ 10%. Nous cherchons donc à savoir quels sont ces 10% pertinents du point de vue des neurosciences.
Qu’est-ce qu’un domaine comme les neurosciences peut apporter à un mathématicien ?
Les neurosciences ne sont pas seulement un domaine d’application des mathématiques, on y trouve des questions mathématiques ouvertes. C’est le cas en EDP, avec des questions d’existence et d’unicité des solutions. C’est aussi le cas en géométrie : la caméra ou l’œil impliquent de la géométrie élémentaire (comme le théorème de Pythagore) mais aussi de la géométrie algébrique très compliquée. Une question touchant à la géométrie est celle de la reconstruction 3D, caractéristique des systèmes multicaméras. Nos deux yeux en sont un exemple : notre cerveau reconstitue l’image 3D à partir de deux images différentes.
Les neurosciences comportent aussi un aspect stochastique, avec des champs de Markov, de la théorie des probabilités, de la théorie de l’information. L’image et la perception visuelle convoquent une grande variété de champs des mathématiques.
Votre intérêt pour les neurosciences va-t-il au delà des questions liées à l’image ?
Oui. Je suis parti des questions de perception visuelle et puis j’ai été amené à m’intéresser à d’autres problèmes de neurosciences. Par exemple : comment fonctionne un neurone ? Comment peut-on décrire mathématiquement ses comportements ? Que se passe-t-il quand on met des neurones en réseaux ? Mon activité principale aujourd'hui est de mathématiser les représentations de ces comportements individuels et collectifs et de confronter les prédictions de mes modèles aux résultats de l'expérience.
Les neurosciences ont-elles besoin des mathématiciens ?
Il existe une énorme demande de formalisation de la part des biologistes du cerveau, qui sont confrontés à des phénomènes très complexes. Les questions mathématiques posées par les neurosciences nécessitent des mathématiques de très haut niveau, que ne maîtrisent ni les biologistes, ni les ingénieurs. Elles relèvent du calcul stochastique, de la théorie des bifurcations, de la théorie des systèmes dynamiques… Par exemple, pour comprendre le fonctionnement d’un neurone, il faut maîtriser la théorie des systèmes dynamiques stochastiques. Il y a un besoin de modélisation, de mise en équation des modèles, d’analyse mathématique de ces modèles. Des mathématiciens doivent répondre à ces besoins mais ce n’est pas encore suffisamment le cas. La théorie des neurosciences est plutôt occupée par des physiciens théoriciens pour le moment, ce qui est très bien, et pas assez par des mathématiciens, ce qui est ennuyeux. Il faudrait que des gens du calibre d’Henri Poincaré fassent des neurosciences.
Un exemple de question ouverte offerte par les neurosciences ?
Un neurone communique avec des milliers d’autres neurones, qui le soumettent à ce qu’on appelle un bombardement synaptique. Ce bombardement synaptique fait varier son potentiel de membrane (qui est la variable d’état d’un neurone) dans le temps. Ces fluctuations sont aléatoires. Quand le potentiel de membrane dépasse un certain seuil, le neurone émet ce qu’on appelle un spike. Comme les variations du potentiel de membrane sont aléatoires, l’apparition d’un spike est aussi aléatoire. Le temps entre deux spikes est donc une variable aléatoire dont on peut essayer de calculer la loi (en fonction des caractéristiques du neurone). Il se trouve que ce calcul est un problème de mathématiques très difficile, que l’on se sait pas encore résoudre dans le cas général.
Est-ce que la formation mathématique incite les futurs mathématiciens à puiser des problèmes, des thèmes de recherche dans d’autres disciplines comme les neurosciences ?
Il y a beaucoup à faire au niveau de la formation. Je donne un cours intitulé « Méthodes mathématiques pour la neuroscience » à l’ENS (dans la filière Math-Info) mais il existe peu de cours de ce genre dans les filières de mathématiques. En France, on a tendance à distinguer mathématiques pures et mathématiques appliquées. Selon moi ce n’est pas ça qui est important. L’important est de faire de bonnes mathématiques, c’est-à-dire des mathématiques rigoureuses, des mathématiques originales, et pourquoi pas des mathématiques utiles au sens où elles font progresser d’autres disciplines. Les travaux d’Alain Connes ont eu un grand retentissement en physique théorique, en mécanique quantique. Il faudrait que des mathématiciens regardent les neurosciences comme Alain Connes a su regarder la physique théorique. Qu’ils y cherchent des questions. Certains mathématiciens vont vers l’ingénierie ou la physique mais pas encore vers les neurosciences. Il est vrai que c’est encore une discipline nouvelle, en train de se créer. Mais il faut savoir qu’elle offre des questions immenses au travail d’un mathématicien.
Pour finir je dirai que les neurosciences comportent énormément d’applications sociétales notamment dans le domaine de la santé ou de la compréhension philosophique de la condition humaine. Elles jouent un rôle dans la compréhension de certaines maladies (Parkinson, par exemple) ou du psychisme (qu’est-ce que la conscience ?). Cette discipline sera amenée à intervenir dans la résolution des problèmes liés au vieillissement de la population (pour pallier la dégradation des facultés cérébrales, par exemple). Les neuroscientifiques travaillent sur des Brain Computer Interface (des interfaces reliant le cerveau et l’ordinateur) destinées à aider des personnes handicapées. Dans un autre ordre d'idées, ces Brain Computer Interface intéressent aussi le monde du jeu : bientôt, on pourra peut-être piloter directement son jeu avec quelques électrodes disposées sur un casque.
The mathematical path of Etienne Ghys
Étienne Ghys est directeur de recherche CNRS à l’Unité de Mathématiques pures et appliquées de l’École Normale Supérieure de Lyon, qu’il a contribué à fonder, et membre de l’Académie des Sciences. Ses travaux touchent plus particulièrement à la géométrie, à la topologie et aux systèmes dynamiques, bien qu’il n’aime guère cloisonner les mathématiques, qui, selon lui, « sont une seule et même chose ». Lorsqu’on lui demande d’énoncer ses domaines de recherche, il préfère répondre tout simplement « je fais des mathématiques ».
Propos recueillis à l'occasion de Maths A Venir 2009.
Vous avez fait vos études de mathématiques à Saint-Cloud ou à Lille ?
J’ai été admis à l’ENS de Saint-Cloud, ce qui, cela dit en passant, signifie que j’ai raté la rue d’Ulm. Aujourd’hui je pense que ce n’était pas une mauvaise chose pour moi car ça m’a remis les pieds sur terre. J’ai cependant vite quitté Saint-Cloud pour l’université de Lille. Je suis profondément provincial, je ne me plaisais pas en région parisienne. Ma formation est donc essentiellement lilloise.
Sur quel sujet portait votre premier travail de recherche, autrement dit votre thèse ?
S’il est vrai que la thèse est en général le premier travail de recherche original dans la carrière d’un mathématicien, cela n’a pas été mon cas. Il se trouve que j’avais déjà effectué un travail sur les feuilletages, que je n’ai pas pu valider comme thèse, mais qui m’a permis d’entrer au CNRS. J’ai donc intégré le CNRS avant ma thèse, ce qui ne correspond pas au parcours habituel. J’ai ensuite fait ma thèse sur les actions de groupes, un sujet qui fait intervenir l’un des concepts les plus importants en mathématiques : le concept de groupe, intimement lié à celui de symétrie. Sans entrer dans le détail de ce que cela signifie, disons qu’il existe ce qu’on appelle des groupes de symétries. Quand un mathématicien regarde un objet mathématique, par exemple un cube, il en observe les symétries qui constituent un groupe. Dans mon travail de thèse, j’ai un peu fait l’inverse : partir d’un groupe de symétries et me demander quels objets possèdent ce groupe de symétries. Ce n’est ni de la géométrie, ni de la théorie des groupes, ni de la topologie, ni des systèmes dynamiques, mais c’est un mélange de tout ça.
Après votre thèse, vous avez eu le privilège d’inaugurer une réforme importante du système universitaire…
Autrefois, après la thèse de troisième cycle, on faisait une thèse d’Etat, c’est-à-dire encore un travail chapeauté par un directeur de thèse. Cet ancien système favorisait beaucoup le mandarinat. Maintenant, après sa thèse de doctorat, on passe une habilitation à diriger les recherches. L’habilitation est un acte individuel : il n’y a pas de directeur qui recommande le jeune chercheur, c’est lui-même qui estime qu’il est assez mûr pour passer son habilitation. Il écrit alors un texte de synthèse où il intègre l’ensemble de ses publications, puis il remet ce dossier au conseil scientifique de son université où des rapporteurs donnent (ou non) leur feu vert pour une soutenance. Je suis arrivé au moment où le système changeait. J’ai eu le choix entre passer soit la dernière thèse d’Etat, soit la première habilitation. J’ai choisi cette dernière et j’ai eu beaucoup de plaisir à rédiger mon rapport d’habilitation. Cela peut être vraiment enrichissant de prendre le temps d’expliquer pourquoi on a réalisé tel ou tel travail.
Comment avez-vous choisi de travailler dans les domaines mathématiques qui sont les vôtres aujourd’hui ?
A Lille, où j’ai suivi mon cursus, j’ai été bien accueilli par des individus qui m’ont donné envie de travailler sur ces sujets. Peut-être que certains mathématiciens font leurs choix de recherches suivant des motifs purement scientifiques mais il me semble que dans la majeure partie des cas, ce sont des choix humains : on est marqué par un professeur, par un maître…
Que vous ont apporté les voyages faits à l’étranger quand vous étiez jeune chercheur ?
Entre la thèse et l’habilitation, j’ai eu la chance de faire deux grands voyages. Le premier a été une coopération scientifique (à la place du service militaire) à Rio, au Brésil. Je suis parti le lendemain de ma thèse pour l’Instituto nacional de matemática pura e aplicada (IMPA). Cela a été extrêmement formateur car j’y ai découvert une autre façon de faire des mathématiques, qui correspondait plus à ma personnalité. J’aime les mathématiques dès qu’elles touchent au qualitatif. C’est pour cette raison que je me sens très à l’aise avec la topologie. Au Brésil j’ai pu faire des mathématiques moins « carrées », moins bourbakistes (NDLR : du nom de Bourbaki, groupe de mathématiciens très influent en France, en particulier dans les années 1960, 1970).
Ensuite, je suis parti aux Etats-Unis, à New York, où j’ai côtoyé un très grand mathématicien : Dennis Sullivan. Il a été véritablement mon maître. Je l’ai vu au travail alors que je n’étais qu’un débutant, ce qui était tout à fait fascinant car il était à l’apogée de sa gloire. Il avait une culture très large, très horizontale, et cette capacité de mettre en contact des disciplines qui a priori n’étaient pas liées. Son approche me plaisait beaucoup. Je comparerais cette expérience avec celle que l’on vit avec un guide de montagne : on fait une promenade avec lui et il nous montre le chemin. Certains très grands mathématiciens n’ont aucun attrait pour le fait d’avoir des étudiants mais d’autres ont une façon de merveilleuse de transmettre le témoin. Gromov (lauréat du prix Abel 2009), par exemple, m’a aussi transmis beaucoup de choses. Pour moi cet aspect transmission est important.
Comment êtes-vous passé de Lille à Lyon ?
La création de l’ENS Lyon entrait dans la logique de la décentralisation et, comme je l’ai déjà dit, je suis très provincial. Je suis arrivé à Lyon un an après la création de l’École, sur la suggestion d’un collègue. Le département de mathématiques était presque vide. Avec quelques collègues nous avons eu la mission de le remplir, c’est-à-dire de trouver des collègues, de recruter des jeunes…
Quelles mathématiques faites-vous aujourd’hui ?
Je travaille en ce moment sur la notion de chiralité. Un objet chiral est un objet qui ne peut pas se superposer à son image dans le miroir. Un exemple immédiat est la main. D’ailleurs, le mot « chirurgie », l’art de la main, a la même racine étymologique que le mot « chiral ». La chiralité est importante en chimie. Certaines molécules sont images chirales l’une de l’autre et ne réagissent pas de la même manière avec d’autres molécules, en particulier les protéines. En topologie, il existe des nœuds chiraux et des nœuds amphichiraux. Déterminer si un nœud est chiral ou pas est un problème de topologie. Moi je m’interroge sur la chiralité non pas des nœuds mais des dynamiques. Il existe des champs de vecteurs (qui sont des systèmes dynamiques) droitiers ou gauchers. Par exemple, quand on observe un fluide qui bouge dans un grand récipient, on peut s’intéresser aux trajectoires de ses particules et dire si ce fluide est chiral ou pas.
Mais j’aimerais ajouter que mon activité de recherche pure occupe moins de place aujourd’hui qu’il y a 20 ans. Au fil de la carrière d’un mathématicien, la profession s’enrichit d’autres choses et c’est aussi ce qu’il y a de formidable avec ce métier, de pouvoir moduler entre ces diverses choses. Mon métier consiste donc aussi à avoir des étudiants, ce que j’aime beaucoup mais qui prend du temps et me laisse moins de temps pour mes mathématiques, ou encore à faire de l’administration (en tant que directeur de laboratoire). Je suis également rédacteur en chef des publications de l’IHÉS : évaluer le travail des autres est aussi un travail mathématique, une manière d’apprendre des mathématiques. Enfin, je contribue à la communication des mathématiques en dehors de la communauté des mathématiciens. Pour moi, toutes ces choses sont importantes.
Pouvez-vous en dire plus sur la communication des mathématiques auprès du grand public ?
J’essaye de faire sortir les maths de la communauté mathématique depuis le début de ma carrière (via des exposés dans les lycées) et de plus en plus. Je pense qu’il y a un gros problème de communication dans le monde mathématique. Je suis assez remonté contre cet hermétisme. Il faut vraiment qu’on fasse des progrès là-dessus. La désaffection des jeunes pour les filières scientifiques est bien réelle. Il y a une diminution des vocations car il existe une vison faussée des mathématiques, de ce qu’est un mathématicien.
Est-ce particulièrement difficile de communiquer sur cette discipline ?
Il n’est pas plus difficile de communiquer sur les mathématiques que sur d’autres disciplines. Mais il faut en avoir envie. Il faudrait aussi que les structures officielles, comme le CNRS ou les universités, reconnaissent que ces activités font partie de notre métier. J’ai encore en tête l’exemple de deux de mes collègues qui n’ont pas jugé opportun de signaler leurs activités de communication des mathématiques dans leur rapport d’activité, comme si c’était honteux ou indigne.
Vous êtes l’un des responsables du site grand public Image des mathématiques. Comment se passe la publication des articles ?
Sur le site, on peut s’inscrire pour être relecteur, mathématicien ou pas. Il y a 5 ou 6 relecteurs par article, qui se livrent à une longue discussion sur l’article en vue de l’améliorer. Le processus de réécriture peut durer jusqu’à trois mois. Quand on estime que l’article est digne d’être publié, c’est qu’il est impeccable.
Comment avez-vous conçu votre film Dimensions ?
Pour illustrer un exposé de mathématiques, j’avais besoin d’images que j’avais choisies sur Internet mais que je ne pouvais pas télécharger. J’avais donc écrit au site en question et j’étais tombé sur Jos Leys. J’ai ainsi fait la connaissance de cet ingénieur chimiste de 55 ans qui ne connaissait pas grand-chose en maths. Je lui ai proposé une collaboration. Dimensions a en quelque sorte été fait pour Jos, pour lui expliquer en images la notion de dimension. Ensuite, Aurélien Alvarez s’est joint à nous. Depuis, le film a été largement vu. Il y a eu 630 000 visites sur le site et le DVD s’est déjà écoulé à 10 000 exemplaires. Il a été traduit en de nombreuses langues. En ce moment il est traduit en zoulou. On a d’ailleurs accès à une carte du monde des connections sur le site. C’est assez émouvant de se dire par exemple que 27 000 personnes en Chine au vu le film.
Avez-vous d’autres projets du même type ?
Un deuxième film est en gestation. Nous hésitons entre une suite du premier et quelque chose d’autonome, de différent. Les idées de thèmes ne manquent pas. Je songe à faire quelque chose de beaucoup plus élémentaire, à viser notamment les enfants. Le premier film n’a pas reçu de soutien des instances officielles pour sa diffusion. Pour d’éventuels projets à venir, j’aimerais disposer de plus de moyens, par exemple pour me faire aider de vrais professionnels de la vidéo.
A voir :
Le site Images des mathématiques : images.math.cnrs.fr.
Le site du film Dimensions : www.dimensions-math.org.
François Loeser ou l'art de l'analogie
 Classes préparatoires au lycée Louis-le-Grand, Ecole Normale Supérieure… François Loeser a suivi le parcours d’étudiant le plus classique pour devenir mathématicien. Entré au CNRS en 1985, il devient ensuite, en 1989, professeur à l’Université Pierre et Marie Curie, puis, de 2000 à 2010, à l’ENS, dont il dirige le Département de mathématiques et applications (UMR 8553 du CNRS). En septembre 2010, il quitte l’ENS pour retrouver l’Université Pierre et Marie Curie et l’Institut de Mathématiques de Jussieu. Entre autres distinctions, il a reçu un Advanced Investigator Grant de l’European Research Council pour la période 2010-2014, une importante récompense au niveau européen, ainsi que la Médaille d'argent du CNRS en 2011.
Classes préparatoires au lycée Louis-le-Grand, Ecole Normale Supérieure… François Loeser a suivi le parcours d’étudiant le plus classique pour devenir mathématicien. Entré au CNRS en 1985, il devient ensuite, en 1989, professeur à l’Université Pierre et Marie Curie, puis, de 2000 à 2010, à l’ENS, dont il dirige le Département de mathématiques et applications (UMR 8553 du CNRS). En septembre 2010, il quitte l’ENS pour retrouver l’Université Pierre et Marie Curie et l’Institut de Mathématiques de Jussieu. Entre autres distinctions, il a reçu un Advanced Investigator Grant de l’European Research Council pour la période 2010-2014, une importante récompense au niveau européen, ainsi que la Médaille d'argent du CNRS en 2011.
Pour en savoir plus, consultez ici sa page personnelle : www.math.jussieu.fr/~loeser/
A l’interface de quatre domaines
François Loeser a commencé sa carrière de chercheur en étudiant les singularités, c’est-à-dire, les points, dans une forme géométrique, où l’on observe une rupture (ces points singuliers sont par exemple les points de rebroussement d’une courbe, ou encore les points où une surface se coupe). Il s’est ensuite intéressé à l’étude des intégrales p-adiques, puis à l’intégration motivique, et enfin à la théorie des modèles. « D’un certain point de vue, je ne suis pas spécialiste d’un domaine donné mais à l’interface de quatre domaines : les singularités, la géométrie algébrique, la théorie des nombres et la théorie des modèles » explique-t-il avant d’ajouter : « Au cours de ma carrière, j’ai eu l’impression d’opérer des changements mais en fait, avec le recul, je me rends compte qu’il y a une unité dans tout ce que j’ai fait. Finalement, même si on augmente le champ des techniques utilisées, on reste sur les mêmes questions. »
Intégrales p-adiques
Classiquement, on calcule des intégrales en utilisant des nombres réels. En pratique, le calcul intégral sert, par exemple, à calculer des aires. En théorie des nombres, d’autres corps que le corps des réels sont apparus. Les corps p-adiques en font partie. (Ici, le p désigne un nombre premier.) Dans l’étude des intégrales, il peut être intéressant de chercher quelles sont les analogies et les différences entre le cas habituel, avec des réels, et le cas p-adique.
Une des découvertes principales de François Loeser, en collaboration avec le mathématicien belge Jan Denef, est qu’en utilisant des intégrales p-adiques, on pouvait démontrer des résultats sur la géométrie des variétés algébriques complexes (autrement dit les lieux des zéros des polynômes à plusieurs variables sur les nombres complexes). « C’est très étonnant car les nombres complexes et les nombres p-adiques sont deux mondes parallèles. Il est surprenant de démontrer grâce aux uns des résultats sur les autres », confie François Loeser. « Cet exemple est au cœur de ma vision personnelle des mathématiques. C’est l’art d’utiliser des analogies en permanence. »
Intégration motivique
Les bases de l’intégration motivique ont été posées en 1995 par Maxim Konsevitch. Ce concept est difficile à appréhender pour le non-spécialiste, mais on peut essayer de s’en faire une idée : « Avant d’intégrer des fonctions, on mesure des ensembles », rappelle François Loeser. « Deux questions qui se posent naturellement sont : quels sont les ensembles que l’on mesure ? et qu’est-ce que la mesure ? Dans le cas habituel, les ensembles sont des parties de Rn et la mesure, un nombre réel positif. Il s’agit donc à chaque fois de nombres réels. Dans l’intégration motivique, il y a une différence de nature entre ce que l’on mesure et là où se situe la mesure. Les ensembles mesurés sont des parties de Kn, où K est un corps de séries formelles, tandis que la mesure est un objet géométrique sur C, le corps des complexes. Avant Konsevitch, on essayait de faire des mesures à valeurs réelles sur ces ensembles de Kn. L’idée fondamentale de Konsevitch a été de remplacer les réels par un anneau construit avec des objets géométriques complexes. »
François Loeser a beaucoup contribué au développement de l’intégration motivique, d’abord avec Jan Denef puis avec Raf Cluckers, un autre mathématicien belge. Cette nouvelle technique a permis de démontrer les résultats évoqués précédemment sur les variétés algébriques complexes sans utiliser les nombres p-adiques mais en utilisant à leur place des séries formelles à coefficients complexes.
« On a tendance à croire que pour étudier quelque chose sur C, on n’a pas besoin de sortir de C », s’amuse François Loeser. « Là, on voit qu’il peut être utile de voir les nombres complexes comme faisant partie d’un corps plus grand : le corps des séries formelles. En travaillant sur ce corps des séries formelles, on obtient les résultats que l’on n’arrivait pas à démontrer sur C. »
L’intégration motivique permet également d’obtenir des résultats d’uniformité sur les intégrales p-adiques quand p varie.
Enfin, un autre exemple d’application de l’intégration motivique est en lien avec le Lemme Fondamental, une conjecture essentielle du programme de Langlands. Le Lemme Fondamental est une égalité entre deux fonctions définies par des intégrales. Il a été établi par Gérard Laumon et Bao Chau Ngo sur les corps de fonctions (qui sont une généralisation du corps des fractions rationnelles en une variable). Ensuite, Jean-Loup Waldspurger (mathématicien français qui a obtenu cette année le très prestigieux Prix Clay) a démontré que si on connaissait le Lemme Fondamental sur les corps de fonctions, on pouvait le déduire sur les corps p-adiques. L’intégration motivique permet de retrouver directement ce résultat de Waldspurger.
Théorie des modèles
Dans ses travaux sur l’intégration motivique, François Loeser utilise de la logique mathématique, et plus précisément un domaine de la logique mathématique qui s’appelle la théorie des modèles, et qui est une façon abstraite de comprendre l’algèbre.
« Il y a toujours eu une forte présence de l’univers non-archimédien et de la géométrie dans mes travaux », remarque le mathématicien. Pour se faire une idée, disons que selon le point de vue non-archimédien, on s’intéresse aux ordres de grandeur plutôt qu’aux mesures exactes. En géométrie non-archimédienne, tous les triangles sont isocèles.
« Quand on fait de la géométrie sur un corps non-archimédien, si on a une approche trop naïve, on se retrouve avec des objets totalement discontinus et donc impossibles à étudier » remarque François Loeser. « En revanche, en ajoutant des points à ces espaces, on obtient, comme l’a observé Vladimir Berkovich, des objets qui ont de bonnes propriétés. Avec Ehud Hrushovski, on s’est aperçu qu’en utilisant de la théorie des modèles très avancée, comme la stabilité, on pouvait démontrer que les espaces introduits par Berkovich ont de bonnes propriétés topologiques dans des cas non connus auparavant. »
Un mathématicien ouvert
Quand on lui demande sur quels problèmes il travaille, François Loeser répond : « Je ne me considère pas comme un problem-solver. Je n’ai jamais l’impression de travailler sur un problème déterminé à l'avance mais plutôt sur de nouvelles techniques, de nouvelles idées, pour découvrir que l’on peut faire des choses intéressantes avec. » Et si on lui demande si ses travaux ont des applications, il rétorque : « Oui, des applications aux mathématiques. »
François Loeser fait partie de ces mathématiciens curieux, qui s’intéressent de près aux recherches de leurs collègues travaillant sur d’autres problèmes que les leurs, voire dans d’autres domaines. Il y trouve aussi bien des applications potentielles pour ses travaux que des sources d’inspiration. « Je ne me suis jamais senti à l’intérieur d’une discipline fixe. Je suis d’ailleurs très content d’être invité à des conférences dont les publics n’ont presque pas d’intersection entre eux. »
Curiosité, ouverture à des thématiques variées sont pour François Loeser des qualités essentielles chez un mathématicien même si, pour conclure, il admet avec humour que « cela rend peut-être plus difficile d'être reconnu par chaque communauté. »
Les Advanced Investigator Grants de l’ERC
C’est la deuxième édition pour ces « grants » financés par la Communauté Européenne, qui subventionnent des chercheurs choisis sur « projet novateur » comportant une « prise de risque ». Les prix comportent deux niveaux : « starting », pour des jeunes chercheurs, et « advanced », tel qu’obtenu par François Loeser. Même si le lauréat souligne qu’« il est difficile d’expliquer sur 20 ou 30 pages ce que l’on va faire les prochaines années », il encourage ses collègues à candidater car les budgets alloués devraient être en augmentation. Celui qu’il recevra pendant 5 ans, de 2010 à 2014, permettra de financer des invitations de collègues et d’experts extérieurs à son laboratoire, des post-docs et des thèses.
Plus d'informations sur le site de l'ERC : cliquez ici.
Artur Avila et les systèmes dynamiques

Artur Avila est né à Rio de Janeiro en 1979. A seize ans, il remporte la médaille d'or des Olympiades Internationales de Mathématiques, à Toronto, puis intègre l'Instituto Nacional de Matemática Pura y Aplicada (IMPA) de Rio, où il commence des études de mathématiques tout en finissant le lycée. Il n'a que dix-neuf ans quand il commence une thèse sous la direction de Welington de Melo. Il la soutiendra en 2001. Il effectue ensuite un postdoc au Collège de France jusqu'en 2003, date à laquelle le CNRS le recrute.
En 2005, il a l'honneur d'assurer le Cours Peccot du Collège de France, sur le thème : Dynamique des cocycles quasipériodiques et spectre de l'opérateur presque-Mathieu.
En 2006, alors âgé de vingt-sept ans, il reçoit deux récompenses prestigieuses : la Médaille de Bronze du CNRS et le Prix Salem, ainsi qu'une bourse de recherche de trois ans du Clay Mathematics Institute, ce qui lui donne l'opportunité de passer plus de temps à l'IMPA.
Directeur de Recherche CNRS depuis 2008 (à seulement vingt-neuf ans, donc), il travaille aujourd'hui entre Rio et Paris.
Au 5e Congrès Européen de Mathématiques, en juillet 2008, il reçoit le Prix de la Société Européenne de Mathématiques pour ses travaux en systèmes dynamiques et en particulier ses contributions sur le Flot de Teichmuller et les échanges d'intervalles.
En juillet 2009, l'Academie des Sciences lui attribue le Grand Prix Jacques Herbrand, qui distingue tous les deux ans un jeune chercheur de moins de trente-cinq ans et dont les derniers lauréats furent Cédric Villani (2007), Franck Barthe (2005) et Wendelin Werner (2003).
Dynamique unidimensionnelle et fractals
Les applications de cette forme p(z) = z2 + c, et plus généralement les applications unimodales (c'est-à-dire qui ont un seul minimum, ou un seul maximum), peuvent apparaître dans certains cas de modélisation en écologie (comme les systèmes proie/prédateur). Dans sa thèse, Artur Avila s’est principalement intéressé au cas où z et c sont des nombres réels. Depuis les années 1970, on sait que la dynamique d'une application unimodale peut être assez compliquée. Quand on observe ce qui se passe quand on itère l’application p(z) = z2 + c, on constate que l’évolution du système dépend, de manière très sensible, du paramètre c. Pour certaines valeurs de c, cette évolution est très régulière (on appellera les paramètres c correspondant les paramètres « réguliers ») et les orbites du système sont attirées par un cycle stable. Pour d’autres valeurs de c, le comportement du système devient « pathologique ». Artur Avila s’est intéressé à la description de ces paramètres non-réguliers. Il a démontré, avec Mikhail Lyubich, Welington de Melo et Carlos Gustavo Moreira, que pour presque tout paramètre non-régulier, la dynamique est très chaotique et semble se comporter comme celle d’un objet aléatoire. Les observations successives ne sont cependant pas totalement indépendantes comme dans le cas d’un véritable objet aléatoire. On parle d’indépendance asymptotique avec une perte de mémoire exponentielle.
Artur Avila a également travaillé sur la dimension de certains ensembles fractals.
Les opérateurs de Schrödinger quasipériodiques
Les opérateurs de Schrödinger quasipériodiques sont des objets qui intéressent en particulier la physique mathématique. Eux aussi font apparaître des ensembles fractals, le plus connu étant le papillon de Hofstadter (Hofstadter's butterfly).

Le papillon de Hofstadter
En 2000, le physicien mathématicien Barry Simon a proposé quinze « problèmes pour le XXIe siècle » qui portaient sur les opérateurs de Schrödinger. Artur Avila a travaillé sur trois d’entre eux, qui tous trois s’intéressent à des propriétés de l’opérateur presque-Mathieu : la conjecture de Hofstadter, auxquels plusieurs travaux avaient été consacrés depuis les années 1980, et qu’Artur Avila a démontrée complètement, avec Raphael Krikorian ; le « Ten Martinis problem » sur lequel Artur Avila a collaboré avec Svetlana Jitomirskaya ; et enfin un troisième problème étudié en collaboration avec David Damanik.
Echanges d’intervalles
Les échanges d’intervalles sont un autre sujet d’étude d’Artur Avila. Prenons un intervalle, coupons-le en deux et échangeons l'ordre des morceaux. Cette opération préserve l'ordre cyclique de l'intervalle. On peut l'imaginer en remplaçant l'intervalle par des cartes à jouer (quand vous "coupez" vos cartes et replacez le tas du dessous au-dessus). Ce découpage en deux est un exemple simple d'échange d'intervalles.
Artur Avila a démontré avec Giovanni Forni que pour presque toutes les façons de couper l'intervalle en quatre, il n'y a aucun « ordre cyclique » non-trivial caché. On dit que l'échange d'intervalle est faiblement mélangeant.
Le flot de Teichmuller
Avec Jean-Christophe Yoccoz et Sebastien Gouezel, Artur Avila a également démontré pour le flot de Teichmuller un résultat assez similaire à celui obtenu sur les applications unimodales : le flot de Teichmuller est très chaotique et, quand on étudie sa dynamique, les observations vérifient également la propriété d’« indépendance asymptotique avec perte de mémoire exponentielle » évoquée précédemment. On dit que le flot de Teichmuller est exponentiellement mélangeant.
Sur le métier de mathématicien
Artur Avila, qui a souvent travaillé avec des co-auteurs, confie apprécier le travail en groupe :
« Pour moi, le travail en groupe est utile pour plusieurs raisons. D’abord, je préfère discuter les mathématiques que de lire les mathématiques. J'aime être confronté au point de vue d'un autre mathématicien, qui peut être assez différent du mien. Et puis ces discussions présentent un autre avantage : au moment où on essaye d’expliquer un aspect d’un problème à quelqu’un, il arrive souvent que l’on voie quelque chose que l'on n'avait pas considéré auparavant. Le seul fait de verbaliser une idée peut déclencher une nouvelle découverte. C'est intéressant également de voir la différence de style entre plusieurs coauteurs. J'aime bien cette partie sociale des mathématiques. »
Maryam Mirzakhani
C'est avec effroi que la communauté mathématique mondiale a appris le décès, le 14 juillet 2017, de la première lauréate de la médaille Fields, Maryam Mirzakhani, âgée de 40 ans seulement. Spécialiste de géométrie et de topologie dont les travaux ont d'importantes répercutions dans l'étude des systèmes dynamiques, son parcours exceptionnel avait commencé en Iran, où elle est née en 1977 et où s'est révélé son talent précoce pour les mathématiques. Médaille d'or aux Olympiades internationales en 1994 et 1995, une thèse très remarquée à Harvard sous la direction de Curtis McMullen, un poste de professeur à Stanford à 31 ans et enfin, le 12 août 2014, à Séoul, la consécration et l'entrée dans l'Histoire avec la Médaille Fields, une première tant pour les femmes que pour son pays d'origine, l'Iran. Un parcours fulgurant qui ne manquera pas d'inspirer aussi bien à l'intérieur de la communauté scientifique qu'en dehors, et en particulier chez les jeunes femmes, ainsi que la mathématicienne en exprimait le souhait lors de l'obtention de la médaille : "je serai heureuse si cela encourage de jeunes femmes scientifiques et mathématiciennes".

©Stanford University
« Plus je passe de temps à faire des maths, plus je suis heureuse. »
Maryam Mirzakhani
Jean-Christophe Yoccoz
Samedi 3 septembre 2016 disparaissait, à 59 ans seulement, l'un des plus grands mathématiciens français contemporains : Jean-Christophe Yoccoz.
Jean-Christophe Yoccoz, c'était l'éternel premier. Médaille d'or aux Olympiades Internationales, premier prix du concours général, reçu premier à l'ENS, classé premier à l'agrégation de mathématiques dans sa jeunesse, il devient, en 1994, lauréat de la Médaille Fields. Professeur au Collège de France, élu à l'Académie des Sciences, Jean-Christophe Yoccoz était aussi membre de l'Académie Brésilienne des Sciences. Il avait beaucoup fait pour les relations scientifiques franco-brésiliennes, nouant dans ce pays de nombreuses collaborations, notamment avec les chercheurs de l'IMPA de Rio de Janeiro. C'est d'ailleurs lui qui, en 2001, avait invité au Collège de France un jeune homme prometteur nommé Artur Avila (Médaille Fields 2014).
La FSMP salue un immense scientifique.
Ceux qui désirent en savoir plus sur Jean-Christophe Yoccoz trouveront dans ce post un florilège (non exhaustif) de textes et de vidéos (articles, interviews, conférences) accessibles, glanés sur le Net.
Hommage d'Images des Mathématiques
Parmi les nombeux articles consacrés à Jean-Christophe Yoccoz dans la presse, celui de Sylvain Crovisier, publié sur le site Images des mathématiques, nous offre un aperçu des contributions majeures du mathématicien. Cliquez ici pour lire cet article.
Interview du CIRM
Interviewé par le CIRM, Jean-Christophe Yoccoz nous invite à découvrir son domaine de recherche, les systèmes dynamiques, et les travaux qui lui ont valu la médaille Fields.
Conférence du 13 avril 2005 à la BnF
Le 13 avril 2005, Jean-Christophe Yoccoz participait au cycle de conférences grand public Un texte, un mathématicien, organisé par la SMF et la BnF, avec un exposé intitulé Une erreur féconde du mathématicien Henri Poincaré. Le texte de cette conférence passionnante avait été publié dans La Gazette des mathématiciens et repris, avec l'aimable autorisation de la SMF, dans la Revue du Collège de France.
Retrouvez ici la page qui lui est consacrée - on peut notamment y télécharger le fac-similé du texte publié.
Entretien du Collège de France : les systèmes dynamiques
Dans ce premier entretien du Collège de France, Jean-Christophe Yoccoz répond à la question "qu'est-ce qu'un système dynamique ?" et laisse éclater son talent de vulgarisateur.
Le nombre de rotations et ses avatars
Voici une vidéo réalisée par l'Institut Henri Poincaré où Jean-Christophe Yoccoz présente une contribution d'Henri Poincaré à la théorie qualitative des équations différentielles.
